Le jeu du marché
A l'origine mis au point par Edward Hastings Chamberlin en 1948, le jeu du marché est un des plus anciens jeux expérimentaux en économie. Vernon Smith, qui était un élève de Chamberlin, introduisit dans le jeu le système de double enchère, et les règles actuelles, les plus courantes, dérivent toutes avec leurs multiples variantes de la version décrite par Charles Holt en 1996.
Notions : offre, demande, marché, concurrence, prix d'équilibre.
Mise en place – déroulement :
La classe est divisée en deux groupes d’élèves numériquement égaux : les uns sont les offreurs et les autres les demandeurs. Les offreurs sont des vendeurs de cochons et sont invités à dessiner un petit cochon, qu’il accrocheront au revers de leur vêtement ; les demandeurs sont des producteurs de jambon, et arboreront un dessin de jambon. La salle est aménagée de manière à laisser au centre un vaste espace libre de circulation, avec les tables et les chaises autour : c’est la place du marché, où se feront les transactions. Les badges des offreurs et des demandeurs permettent alors aux acteurs de se repérer tout en étant libres de leurs mouvement sur la place du marché. Le professeur a également besoin d’un ou deux jeux de cartes à jouer ordinaires ; il n’utilisera que les cartes numérotées de 1 à 10, rouges et noires. La place est bouclée par le bureau du professeur, qui enregistrera les transactions. Il est recommandé, à cet effet, d’utiliser un logiciel du type tableur. Le jeu se déroule en plusieurs tours de 2 à 3 minutes. Au début de chaque tour, chaque offreur se voit remettre une carte rouge, dont la valeur indique le coût de production d’un cochon : il lui est donc interdit de vendre son cochon à un prix inférieur à la valeur de la carte. Chaque demandeur se voit offrir une carte noire dont la valeur représente le prix de vente du jambon déjà négocié auprès de ses clients : il lui est donc interdit d’acheter un cochon à un prix supérieur à cette valeur. Le tour est chronométré, les élèves doivent former un couple offreur-demandeur et faire enregistrer leur transaction avant l’issue du tour. Ils rendent ensuite leurs cartes. Le professeur fait un petit bilan du tour (nombre de transactions, meilleur vendeur, meilleur acheteur), mélange les cartes, les redistribue, et lance un nouveau tour. Le professeur peut mettre fin au jeu au bout de 6 ou 8 tours, c’est le nombre suffisant pour mettre en évidence un équilibre de marché.
Conclusion – interprétation :
Dans le cas d'une classe de 20 élèves, la distribution de 10 cartes rouges et 10 cartes noires numérotées de 1 à 10 donne le schéma théorique d’offre et de demande suivant :
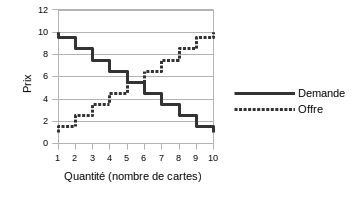
Le prix d’équilibre se situe donc entre 5 et 6.
Le jeu du marché présente un très fort degré de prédictibilité. Au bout de 6 à 8 tours, on s'aperçoit que les transactions tendent à se rapprocher du prix d'équilibre.
A voir :
- La Cité de l'économie propose une version complexisée, avec appli à télécharger.
- Lire l'article de Charles Holt de 1996 et les règles originales du jeu (en anglais).
Le jeu des biens collectifs
Appelé aussi jeu des biens publics, c'est, avec le jeu du marché, le jeu expérimental le plus utilisé en économie. Le jeu a été développé dans les années 1990, et il en existe de nombreuses variantes. Toutes s’appuient pour l’essentiel sur les règles définies par Charles Holt et Susan Laury en 1997 (« Classroom Games: Voluntary Provision of a Public Good », Journal of Economic Perspectives, 1997, #11).
Notions : biens collectifs, dilemme du prisonnier, passager clandestin.
Mise en place – déroulement :
Le jeu peut être joué en classe entière, il nécessite très peu de matériel et de mise en place. Le professeur a besoin d’une urne (un carton de papier à photocopier suffit) et d’un jeu de carte ordinaire (ou deux jeux, si la classe est nombreuse). On suppose que les élèves constituent une cagnotte pour financer un achat collectif.
À chaque début de tour, le professeur donne à chaque élève deux cartes rouges et deux cartes noires. Puis il demande simplement de dépose deux cartes dans l’urne. Le choix est secret, strictement individuel, et les élèves n’ont pas le droit de communiquer. Une carte rouge rapporte 4 points individuellement à celui qui la garde en main, et 1 point à tout le monde si elle est déposée dans l’urne. Une carte noire ne rapporte rien. L’objectif du jeu est de maximiser son profit individuel.
Après une dizaine de tours, on peut révéler les gains individuels et engager la discussion.
Conclusion – interprétation :
Le jeu des biens collectifs est une forme de dilemme du prisonnier. Il admet donc une solution unique offrant un profit optimum (équilibre de Nash). Supposons qu’on joue avec une classe de 30 élèves. Les solutions extrêmes suivantes peuvent se présenter :
-
L’élève Y garde ses deux cartes rouges, et tous les autres déposent leurs cartes rouges dans la cagnotte : dans ce cas, Y gagne 8 + 56 = 64 points, et tous les autres élèves gagnent 56 points. Le gain collectif total est de 64 + (56 x 29) = 1688 points.
-
L’élève Y garde ses deux cartes noires, et tous les autres gardent leurs cartes rouges : Y gagne 2 points, et tous les autres gagnent 10 points. Le gain collectif total est de 292 points.
-
Tous les élèves gardent leurs cartes rouges : tout le monde gagne 8 points. Le gain collectif total est de 240 points.
-
Tous les élèves déposent leurs cartes rouges : tout le monde gagne 60 points. Le gain collectif total est de 1800 points.
Evidemment, des solutions intermédiaires sont possibles, mais le gain maximum individuel est atteint dans la situation a, alors que le gain maximum collectif est atteint dans la situation d, qui correspond à l’équilibre de Nash, ainsi qu’à un optimum de Pareto : c’est la situation où aucun élève ne peut augmenter son profit individuel sans dégrader le profit collectif.
Chaque élève est donc confronté à un dilemme : il comprend que donner permet d’augmenter le gain de tous, mais en même temps, il est tenté de garder ses cartes rouges en espérant que les autres donnent, ce qui lui permet de maximiser son profit individuel (situation a) : l’élève individualiste maximisateur devient, par choix rationnel, un passager clandestin. Or, si chacun a le même raisonnement individualiste maximisateur, on tend à se rapprocher de la situation c.
Voir aussi :
J. VILLON, « Les expériences pédagogiques : vers une méthode active et efficace », IDEES économiques et sociales, n°163, 2010/3.
Le jeu du réservoir
Ce jeu est une variante du jeu des biens collectifs. Elle a été développée par Jean-Philippe Zanco (lycée Le Garros) pour expérimenter la théorie de la tragédie des communs, et proposée en formation académique, en 209 et 2020. Coralie Chartreux (lycée Déodat-de-Séverac) a perfectionné la variante et propose des cartes "truites" et "poissons-chats" à télécharger et imprimer.
Notions : biens communs, tragédie des communs, externalités, incitation, politique environnementale.
Préparation du jeu
La classe est séparée en deux groupes. Les élèves, qui jouent le rôle de pêcheurs, s’installent en cercle autour d’un "lac" (un carton de photocopie peut faire l'affaire) qu’ils disposent au centre de leur table. Les cartes « poissons » sont disposées face retournée dans le lac. Le lac comprend au départ 2 cartes « poisson chat » et deux cartes « truite » par élève. Exemple : s’il y a 10 pêcheurs autour du lac, le lac doit comprendre 20 cartes « truite » et 20 cartes « poisson-chat ».
A défaut de cartes "poissons", on peut aussi utiliser des cartes à jouer ordinaires : les cartes rouges seront les truites et les cartes noires les poissons chats. Seule la couleur compte ici, la valeur faciale n'a aucune importance.
But du jeu
Les pêcheurs pêchent dans un lac aux ressources limitées dans lequel se trouvent deux espèces de poissons : la truite, considérée comme un poisson de valeur (pour sa chair) et le poisson-chat, considéré comme une espèce invasive et nuisible (entre autres puisqu’il se nourrit des œufs des autres poissons). L’objectif de chaque pêcheur est de cumuler le maximum de points grâce à la pêche de poissons.
Déroulement du jeu
Lors d’un tour de jeu, chaque pêcheur peut pêcher dans le lac de 0 à 4 cartes poisson, mais il ne peut pas garder toutes ses prises et doit donc en rejeter dans le lac (remarque : sa pêche et ses rejets doivent rester secrets et doivent donc se faire face cachée pour ne pas être vus par les autres pêcheurs).
Le nombre de poissons à rejeter dans le lac dépend du nombre de poissons pêchés :
- Pour 1 poisson pêché, rejeter 0 carte
- Pour 2 poissons pêchés, rejeter 1 carte
- Pour 3 poissons pêchés, rejeter 1 carte
- Pour 4 poissons pêchés, rejeter 2 cartes
Calcul des points
A la fin d’une manche, qui comprend 3 tours de pêche, chaque pêcheur compte les points qu’il a dans son jeu. Mais il faut également tenir compte des atteintes portées à l’écosystème du lac en comptabilisant collectivement les points présents dans le lac. La valeur des cartes « poisson » dépend du fait qu’elles se trouvent dans le jeu d’un pêcheur ou bien dans le lac.
Valeur des cartes :
Carte « poisson-chat » :
- 0 point pour le joueur qui l’a dans son jeu
- - 1 point pour tous les joueurs lorsqu’il est dans le lac
Carte « truite » :
- 4 points pour le joueur qui l’a dans son jeu
- 1 point pour tous les joueurs lorsqu’elle est dans le lac
Remarque : s’il ne reste aucun poisson dans le lac à la fin de la partie, tous les joueurs reçoivent une pénalité de 5 points pour surexploitation d’une ressource naturelle.
Le vainqueur
Le vainqueur de la partie est celui qui obtient le maximum de points en additionnant ses points et ceux du lac au cours des 2 manches de jeu.
CONCLUSION - INTERPRÉTATION - DÉBAT
A la fin de la partie, on demande aux élèves de consigner par écrit leurs constatations, et de proposer des solutions pour préserver la ressource et les profits :
"Face à la prise de conscience générale sur la nécessité de préserver la biodiversité du lac, vous décidez d’organiser une réunion entre tous les pêcheurs afin de mettre en place des mesures pour éviter la surexploitation des truites. Votre nouvelle contrainte est de garder 2 truites dans votre lac à la fin de chaque manche pour permettre aux truites de se reproduire et ne pas épuiser la ressource. "
Quelles sont les mesures que vous avez choisies collectivement ?
- ...
- ...
- ...
Quelles sont les nouvelles règles du jeu permettant d’appliquer vos mesures pour la deuxième partie ?
- ...
- ...
- ...
On propose ensuite une deuxième partie plus carte (une manche suffit) pour expérimenter l'efficacité des mesures.
Cartes à télécharger :


Le jeu des rendements décroissants
Cette version du jeu des rendements décroissants est très simple et très amusante. Elle a été mise au point par un professeur d'économie australien, Wayne Gerling. On peut en voir le déroulement filmé par Geerling sur YouTube.
Notions : croissance, productivité, productivité marginale, rendements décroissants.
Mise en place - déroulement :
Comme matériel, munissez-vous d’une boîte en carton (type carton de papier à photocopier) ou d’une corbeille à papier, et d’une vingtaine de balles de tennis (personnellement, je remplace tout simplement par des boulettes de papier froissé).
Le professeur a besoin de douze de cobayes volontaires. Il les place devant le tableau, en file indienne. À une extrémité de la file, il place le carton. À l’autre extrémité, il place un autre volontaire, à qui il confie les balles de tennis.
Un tour dure trente secondes. Le professeur lance le chronomètre (avec classroomscreen, par exemple). Le volontaire en charge du sac passe une balle au premier élève, et les élèves doivent se passer la balle de main en main, jusqu’à la corbeille. Il est interdit de lancer les balles, il est interdit de se déplacer, il est interdit de se passer plus d’une balle à la fois. À la fin du tour, on compte les points : chaque balle dans la corbeille rapporte 4 points, mais chaque élève de la file engendre un coût salarial de 2, et le jeu lui-même a un coût fixe de participation de 5.
Au tour suivant, le professeur renvoie deux élèves de la file, puis deux encore au tour suivant, et ainsi de suite, de façon à obtenir les résultats de l’expérience pour 12, 10, 8, 6 et 4 élèves.
Il est utile que le professeur ait prévu à l’avance un tableau numérique permettant de consigner les résultats, sur le modèle suivant (le nombre de balles est donné à titre d’exemple) :
Nombre d'élèves |
Nombre de balles dans la corbeille |
Coût total du tour |
Bénéfice total du tour |
Bénéfice marginal |
4 |
14 |
(4 x 2) + 5 = 13 |
(14 x 4) - 13 = 43 |
- |
6 |
18 |
(6 x 2) + 5 = 17 |
(18 x 4) - 17 = 55 |
8 |
8 |
19 |
(8 x 2) + 5 = 21 |
(19 x 4) - 21 = 55 |
0 |
10 |
13 |
(10 x 2) + 5 = 25 |
(13 x 4) - 25 = 27 |
-28 |
Ce tableau peut aussi être retranscrit en graphique. Le jeu des balles de tennis permet de représenter la loi des rendements décroissants, avec un fort degré de prédictibilité.
Sellacar : le jeu du marché des tacots
"Sellacar" est un jeu mis au point lors d'une session de formation dans l'académie de Nancy-Metz en 2018-2019, pour tester la théorie des asymétries d'information en ludifiant le célèbre texte d'Akerlof sur le "market of lemons". Le détail du dispositif ci-dessous, et les premiers tests, sont l'oeuvre de Franck Moine, du lycée Pierre d'Aragon à Muret.
Notions : marché imparfait, asymétrie d'information, défaillance de marché, sélection adverse.
Mise en place
Le jeu comporte 15 cartes doubles en couleur (disponible ci-dessous et à plastifier pour plus de commodité) avec des modèles de voitures d’occasion. 8 de ces voitures sont des tacots avec des vices cachés plus ou moins graves.
A leur recto, les cartes vendeurs sont vertes, les cartes acheteurs sont bleues.
Les cartes présentent à leur verso des caractéristiques communes mais ne spécifient que sur la carte vendeur le vice caché s'il y en a un. Seule la carte acheteur précise le prix de réserve de ce dernier. Au vendeur de déterminer son propre prix de réserve. (Si les élèves ont déjà pratiqué le jeu du marché, ils sont coutumiers de la notion de prix de réserve, il suffira juste de vérifier que c'est bien clair pour eux avant de commencer le jeu. Il sera nécessaire d'en repréciser le sens dans le cas contraire).
Contrairement au jeu du marché, le jeu ne nécessite pas de reconfiguration spatiale. Les élèves sont assis et constituent des binômes ou des trinômes (en cas de nombre d’élèves impair, on aura un couple d’acheteurs face à un vendeur seul). Il est cependant recommandé de déplacer les élèves pour éviter que les binômes soient faits de camarades qui se connaissent trop bien, ce qui pourrait un peu fausser le jeu du bluff et de la négociation.
On détermine en premier lieu le rôle de chacun (vendeur ou acheteur), rôle qu’il conservera pendant tout le jeu. On peut avoir recours au tirage au sort, ou à l’entente entre élèves. Puis on distribue les cartes « vendeur » et « acheteur ». Il faut préciser aux élèves qu'ils doivent se garder de montrer leur carte à leur vis à vis car elles ne contiennent pas les mêmes informations. Il est sous-entendu que les vendeurs peuvent omettre de parler de certaines caractéristiques du produit. (En général, les élèves le comprennent bien une fois les cartes en main. Il est parfois nécessaire de préciser à l'un(e) d'entre eux (elles) qu'il ne faut pas évoquer le vice caché devant le vendeur).
Un compte à rebours (avec sonnerie) de 5 mn est affiché au tableau (par exemple, avec Classroomscreen).
Déroulement du jeu
Le premier round de négociation débute : lorsqu'une transaction est réalisée, les élèves se rapprochent du professeur qui collecte sur un fichier tableur ad hoc le prix de vente/achat. Si acheteurs et vendeurs ne parviennent pas à se mettre d'accord sur le prix, le vendeur peut se retirer. Quand la transaction est réalisée, le vendeur révèle sa carte à l’acheteur, et chacun calcule son bénéfice ou sa perte.
-
Pour le vendeur, le bénéfice réalisé est égal à la valeur réelle du véhicule (en enlevant la moins-value liée à un vice éventuel) moins la valeur de l’argus.
-
Pour l’acheteur, le bénéfice réalisé est égal à son prix de réserve moins la valeur d’achat, et en ajoutant le coût des vices cachés éventuels.
La sonnerie retentit et clôt le premier round.
Trois tours sont suffisants pour boucler le jeu et dresser le bilan en une heure. Le professeur veillera que son fichier tableur lui permette de calculer automatiquement :
- le prix moyen des transactions du tour
- le nombre de voitures vendues dans le tour
- le % de tacots dans les transactions réalisées.
Entre chaque tour, il est utile de déplacer les élèves pour reconstituer les binômes, mais les vendeurs et les acheteurs conservent leur rôle. Le professeur redistribue les cartes.
Conclusion - interprétation
La liste des voitures concernées par les vices cachés est affichée, le professeur fait le bilan des voitures vendues et des échecs de négociation et invite les élèves à réfléchir sur ce que le jeu vient de mettre en évidence.
L'objectif étant bien sûr, de vérifier, que les propriétaires de véhicules « tacots » restent sur le marché et que les propriétaires de bons véhicules se retirent du marché, les « mauvais risques chassant les bons ».
En général, on assiste entre le premier et le troisième tour à une baisse du prix moyen des transactions et à une baisse du nombre d’échanges, avec une assez forte prédictibilité. Ce point est déjà suffisant pour valider la théorie d’Akerlof. En général, le % de tacots dans les transactions a aussi tendance à augmenter entre les trois tours, mais la prédictibilité est moins forte : si cela est observé, néanmoins, on aura complètement illustré le texte original d’Akerlof sur le « market of lemons ».
Il est également intéressant d'attirer l'attention des élèves sur le fait que l'asymétrie d'information n'est pas de même nature lorsque le bien propose un vice caché mal réparé voire non réparé par rapport aux véhicules dont le vice a été réparé.
Enfin, on peut discuter avec les élèves des solutions pour éviter les écueils rencontrés par certains acheteurs malchanceux dans le jeu : on évoquera l’intervention de l’État et le droit de la consommation.
Pour finir, la séance peut se terminer par l'introduction de la notion de sélection adverse.
Le concours de beauté
Ce jeu (dit aussi « guessing game ») s’inspire d’un célèbre passage du chapitre 12 de la Théorie générale de l’emploi, de l’intérêt et de la monnaie (1936) de Keynes, dont voici l’extrait :
« [L]a technique du placement peut être comparée à ces concours organisés par les journaux où les participants ont à choisir les six plus jolis visages parmi une centaine de photographies, le prix étant attribué à celui dont les préférences s’approchent le plus de la sélection moyenne opérée par l’ensemble des concurrents. Chaque concurrent doit donc choisir non les visages qu’il juge lui-même les plus jolis, mais ceux qu’il estime les plus propres à obtenir le suffrage des autres concurrents, lesquels examinent tous le problème sous le même angle. Il ne s’agit pas pour chacun de choisir les visages qui, autant qu’il en peut juger, sont réellement les plus jolis ni même ceux que l’opinion moyenne considérera réellement comme tels. Au troisième degré où nous sommes déjà rendus, on emploie ses facultés à découvrir l’idée que l’opinion moyenne se fera à l’avance de son propre jugement. Et il y a des personnes, croyons-nous, qui vont jusqu’au quatrième ou au cinquième degré ou plus loin encore. »
En anglais, si vous voulez travailler en bidisciplinarité (ou avec des élèves motivés) :
" [P]rofessional investment may be likened to those newspaper competitions in which the competitors have to pick out the six prettiest faces from a hundred photographs, the prize being awarded to the competitor whose choice most nearly corresponds to the average preferences of the competitors as a whole; so that each competitor has to pick, not those faces which he himself finds prettiest, but those which he thinks likeliest to catch the fancy of the other competitors, all of whom are looking at the problem from the same point of view. It is not a case of choosing those which, to the best of one’s judgment, are really the prettiest, nor even those which average opinion genuinely thinks the prettiest. We have reached the third degree where we devote our intelligences to anticipating what average opinion expects the average opinion to be. And there are some, I believe, who practise the fourth, fifth and higher degrees."
Rosemarie Nagel, de l’université de Barcelone, a mis au point le protocole expérimental suivant dans les années 1990.
Mise en place – déroulement :
On annonce aux élèves qu’on organise un concours : le but est de deviner un chiffre à l’avance, et le gagnant gagnera un carambar (on fera plusieurs tours, on peut donc gagner plusieurs carambars).
A chaque tour, chaque élève écrit sur une feuille de papier un nombre entre 0 et 100. Le professeur recueille les réponses, et fait la moyenne (il est fortement recommandé de prévoir d’utiliser un tableur, pour que le calcul de la moyenne soit instantanément fait, à mesure que les réponses sont entrées).
Le gagnant est celui dont le nombre est le plus proche de la moitié de la moyenne.
Conclusion - interprétation :
En fait, tous les élèves peuvent gagner : il suffit qu’ils choisissent tous le chiffre « 0 ». « 0 » est le seul résultat qui permet à tout le monde de gagner, sans perte : c’est un équilibre de Nash. Or, dans la réalité, l’expérience montre que la moyenne des résultats observés se situe entre 25 et 35, et qu’il y a, le plus souvent, un seul gagnant.
Ce résultat est dû au fait que les acteurs ne sont pas rationnels, ou plutôt, que leur rationalité est limitée. Dans cette situation, ils essaient d’anticiper ce que les autres vont écrire, ce qui les amène à s’approcher d’une valeur « moyenne » ; ou alors, ils répondent au hasard.
Note - prolongement :
Le manuel Hachette de terminale (éd. 2020) propose une version plus proche d'un "vrai" concours de beauté, au cours de laquelle il faut choisir entre des photos de bébés animaux (p. 104).
Les jeux expérimentaux ne sont pas exactement des jeux sérieux. Ils sont issus de protocoles expérimentaux développés en université dans le cadre de l'économie expérimentale, et ils ont été adaptés et simplifiés dans un but essentiellement pédagogique. Très présents dans les universités et les high schools aux Etats-Unis depuis une vingtaine d'années, ils commencent à se développer en France. Leur intérêt pédagogique essentiel est de pourvoir appliquer la démarche d'investigation hypothético-déductive à l'enseignement des SES.