Un exemple concret de mise en œuvre d’un problème en classe de 1ère.

Objectif :

Proposer des temps dédiés à la résolution problèmes en classe et mettre en œuvre une stratégie de résolution classique de problème : décomposer un problème en sous-problèmes.

Enoncé :

Une entreprise de ferronnerie doit réaliser un portail dont chaque vantail mesure 2 mètres de long.

Le bord supérieur du vantail de droite du portail est modélisé avec une fonction f définie sur l’intervalle [0 ;2] par : f(x) = 2/(2+x²)

Image

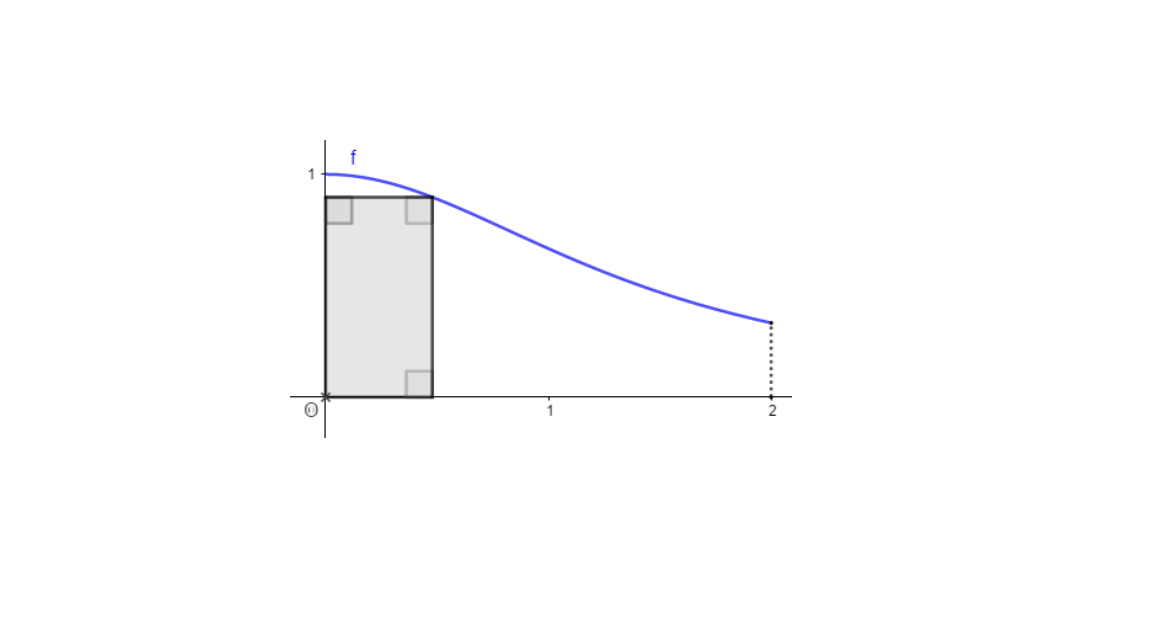
Et chaque vantail doit être renforcé par une pièce métallique en acier de forme rectangulaire, qui s’inscrit dans le vantail comme dans la figure suivante. Les dimensions de la pièce peuvent varier.

Pour des questions de résistance du portail, la pièce métallique doit avoir la plus grande aire possible.
Quelles doivent alors être ses dimensions ?

Contexte :

Cet exercice est un problème qui peut être posé comme exercice bilan du chapitre Dérivation – Point de vue global du programme de l’enseignement scientifique de 1^ère.

C’est un problème pour lequel une recherche d’extrémum est demandé, et qui conduira les élèves à étudier le signe de la dérivée d’une fonction qui modélise la situation.

Modalités de mises en œuvre :

• En début de séance : un automatisme pour réactiver le lien entre variations d’une fonction et le signe de sa dérivée. Durée : 10 minutes.

Enoncé :

Soit f une fonction dérivable sur [-3;2]. On a tracé ci-dessous la courbe représentative C' de la fonction dérivée f'.

Image

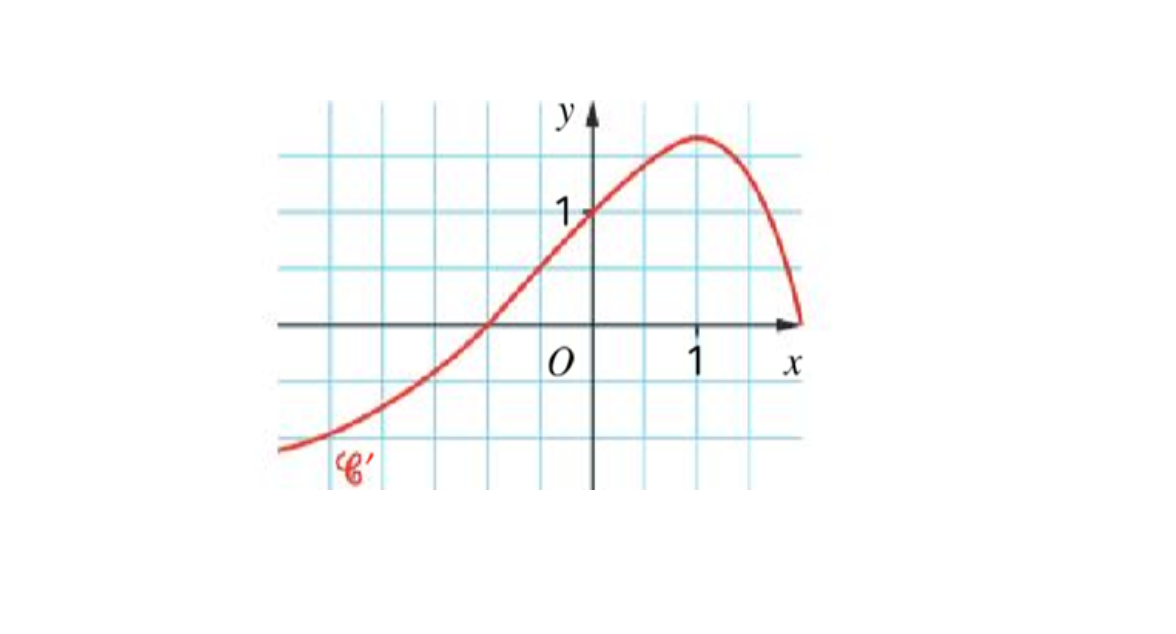
Dire si les affirmations suivantes sont vraies ou fausses :

Affirmation n°1 : f est croissante sur l’intervalle [-1;2]

Affirmation n°2 : f admet un maximum en x=1.

Remarques : l’énoncé est vidéoprojeté, et après 5 minutes de recherche, après un sondage dans la classe, la correction peut s’appuyer sur des élèves qui ont commis les erreurs attendues : confondre les variations de f avec celles de f'.
Bilan de la méthode qui sera utilisée dans l’activité : Pour étudier les variations d’une fonction dérivable, on peut étudier le signe de sa dérivée.

• Activité (40 minutes) :

Un exemple de mise en œuvre de cette activité pourrait être le suivant :

• Lecture silencieuse de l’énoncé à l’issue de laquelle un élève reformule la question. Pour faciliter la compréhension de problème, l’enseignant peut utiliser un logiciel de géométrie dynamique et montrer une animation de la situation (voir fichier en pièce jointe).
• Premier temps de recherche en autonomie pendant 5 minutes.
• Un premier point avec la classe pour dégager les pistes et débloquer les élèves qui n’auraient pas démarré : il faut étudier les variations de l’aire du rectangle, pour cela, on peut exprimer l’aire du rectangle en fonction de l’un de ses côtés. On peut poser OB=x
• Deuxième temps de recherche (5 minutes).
• Un deuxième point avec la classe pour corriger l’expression de la fonction à étudier. La correction peut être faite par un élève à l’oral. L’élève explique sa production et justifie comment il a trouvé l’expression de l’aire du rectangle.
  Questions à poser : Préciser l’ensemble de définition ? Que reste-il à faire ensuite ?
• Dernier temps de recherche : (10-15 minutes) pour dériver la fonction, étudier les variations et conclure.
• Dernier point avec la classe : Correction Chingview ou visionneuse par un élève. Il commente sa production, on corrige les erreurs, et la rédaction qui peut manquer de rigueur.

Pour conclure, on peut demander à un élève de faire à l’oral un bilan de la méthode pour étudier les extrema d’une fonction dérivable et plus généralement, un bilan de la méthode pour résoudre un problème : on le décompose en sous-problèmes.

Fichiers joints :

• Enoncé de l’activité et éléments de correction  

  Enoncé et éléments de correction.docx (42.66 Ko)
• Fichier géogébra animation

https://www.geogebra.org/classic/r4vukyhn

• Enoncé de l’automatisme 

  Automatismes.docx (150.87 Ko)

Pour aller plus loin :

Dans le cadre du plan maths pour le collège, un guide de la résolution de problèmes mathématiques a été publié. Si les exemples et les situations traités sont de niveau collège, le guide développe des démarches didactiques plus théoriques qui permettront aux enseignants de prendre du recul sur leurs pratiques et pourra donc intéresser des enseignants en lycée.

https://eduscol.education.fr/document/13132/download?attachment