Des démonstrations au collège
Constat :
Le BOEN n°31 du 30 juillet 2020 est explicite sur certaines démonstrations attendues en cycle 4.
« Il est attendu de démontrer au moins une propriété du calcul fractionnaire en utilisant le calcul littéral et la définition du quotient. »
Pour le reste du programme, il n’est pas toujours évident de choisir quelles démonstrations faire avec des élèves de collège, comment mener ces démonstrations et de repérer quelles sont celles abordables au collège.
Objectifs de ce focus :
- Faire une liste (non exhaustive) de démonstrations abordables en cycle 4
- Proposer un support de démonstration du théorème de Pythagore
- Proposer deux démonstrations de l’égalité des produits en croix.
- Liste de démonstration abordables en cycle 4
Voici un document qui rassemble des démonstrations de cours qu’il est possible de faire au collège.
Ces démonstrations peuvent être choisies par équipe enseignante et peuvent même être intégrées à la progression commune de l’équipe.
Ce document permet non seulement d’en faire la liste mais aussi propose quelques-unes de ces démonstrations.
Il ne s’agit pas de modèle mais de piste de réflexion.
En numération, beaucoup de ces démonstrations reposent sur la définition du quotient et sur l’unicité du quotient. Ce type de raisonnement prend davantage de sens pour les élèves s’ils le rencontrent à plusieurs reprises, au cours du cycle 4 notamment.
Suivant le niveau des élèves et leur formation à la démonstration, certaines démonstrations pourront s’appuyer sur un exemple générique, tout en précisant que le raisonnement proposé peut se généraliser à d’autres nombres.
Ces choix peuvent être faits par équipe pour y apporter une cohérence et une évolution tout au long du cycle 4.
- Démonstration du théorème de Pythagore
Une activité d’introduction permet de faire découvrir l’égalité de Pythagore.
Voici par exemple celle proposée par le manuel « Mission Indigo 4ème » aux Editions Hachette Education (2016) :

L’objectif de cette activité est de faire apparaître cette égalité de Pythagore et l’image mentale des carrés tracés à partir des trois côtés du triangle rectangle.
La question 3) de l’activité ne permet pas vraiment de faire émerger l’égalité pour tous les triangles rectangles proposés par les élèves. En effet les imprécisions de mesures de longueurs font apparaître que le carré de la longueur de l’hypothèse donne une valeur proche de la somme des carrés des longueurs des deux autres côtés.
Afin de valider ou non cette égalité il apparaît alors nécessaire de travailler avec un triangle rectangle dont les longueurs ne sont pas des valeurs numériques décimales ou entières choisies par les élèves mais de travailler avec un triangle rectangle dont les côtés mesurent a, b et c qui représentent des nombres strictement positifs.
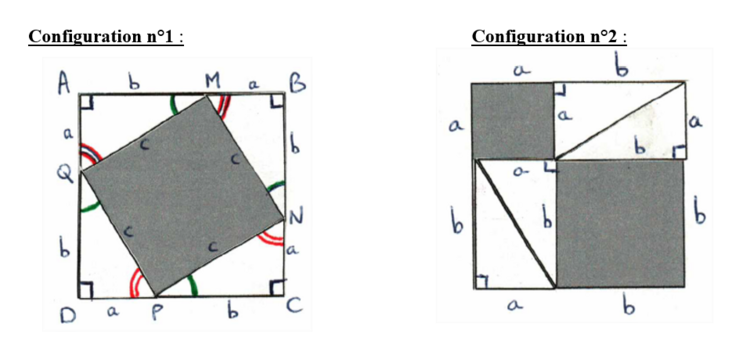
Voici un support de démonstration du théorème de Pythagore avec 8 petits triangles rectangles à découper au préalable :
Voici ce que donnent les configurations une fois les triangles collés :
- Démonstrations de l’égalité des « produits en croix »
Voici un document qui propose deux démonstrations différentes de l’équivalence dite « des produits en croix » :
Ces deux démonstrations reposent sur des prérequis différents. Le choix de l’une ou de l’autre peut être fait en fonction de la progression de l’équipe.
A consulter également :
- Document d’accompagnement sur la place de la compétence « raisonner » en cycle 4 (mars 2016)
- Document d’accompagnement des programmes de mathématiques « raisonnement et démonstration » (mars 2016 mais s’appuyant sur un document de juin 2009).
Pour aller plus loin :
De nombreuses ressources sur le thème « Démonstrations au cycle 4 » sont disponibles sur le site académique en suivant ce lien :
https://pedagogie.ac-toulouse.fr/mathematiques/le-document-quelques-demonstrations-au-cycle-4