L’introduction du théorème de Thalès en 4ème, en 3ème
Constat :
Pas toujours facile d’introduire le théorème de Thalès en classe de 4ème (triangles emboîtés) ou en classe de 3ème (configuration « papillon »), tout en faisant le lien avec les notions de proportionnalité, d’agrandissement-réduction, les triangles semblables, les homothéties, … et de savoir par quel bout le prendre !
Objectifs de ce focus :
- Proposer une activité pour introduire le théorème de Thalès impliquant les élèves
- Aider à construire une progression permettant de faire le lien entre triangles semblables, agrandissements-réductions, théorème de Thalès, homothéties, réciproque du théorème de Thalès, rapports trigonométriques, fonctions linéaires
- Choisir les démonstrations à proposer aux élèves et la forme sous laquelle les travailler.
Activité d’introduction au théorème de Thalès :
Elle est tirée d’un document créé par l’IREM d’Aquitaine et d’Orléans.
1ère étape :
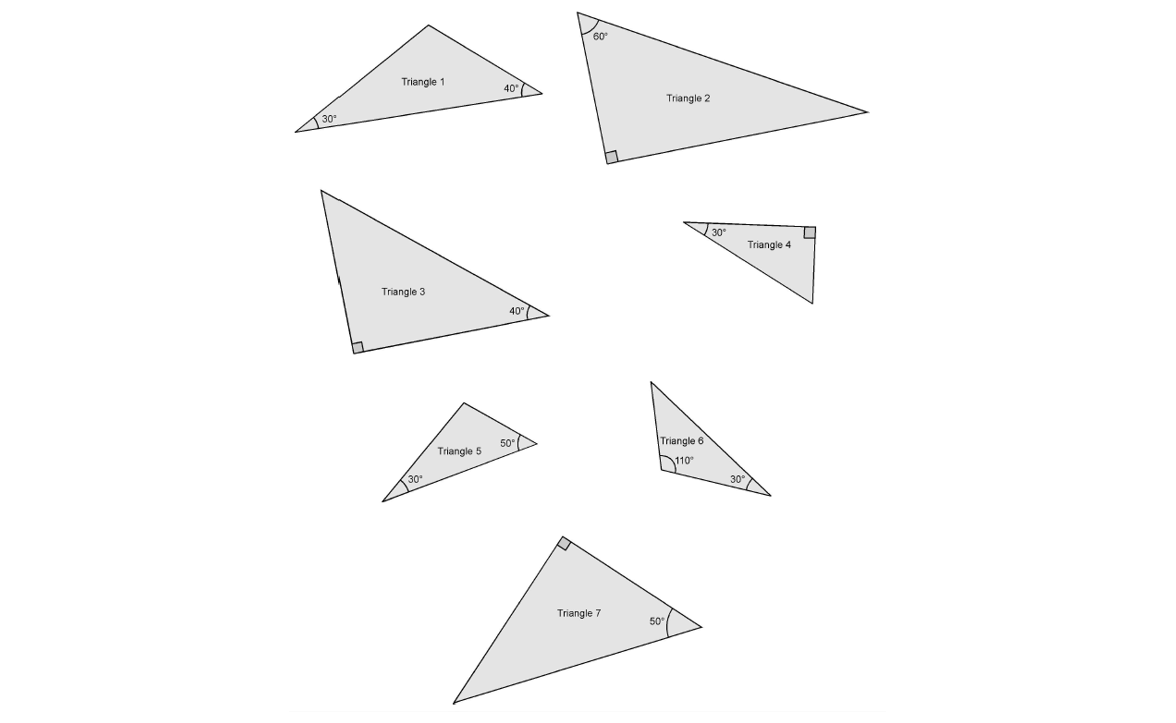
Découper les 7 triangles et retrouver ces trois paires. Aucune mesure n’est permise. Justifier les choix qui ont été effectués, éventuellement par des calculs, mais sans effectuer aucune mesure. Superposer les triangles de manière à rendre les associations visibles. Appeler le professeur quand c’est terminé.
Décrire les couples de triangles formés :
|
2ème étape :
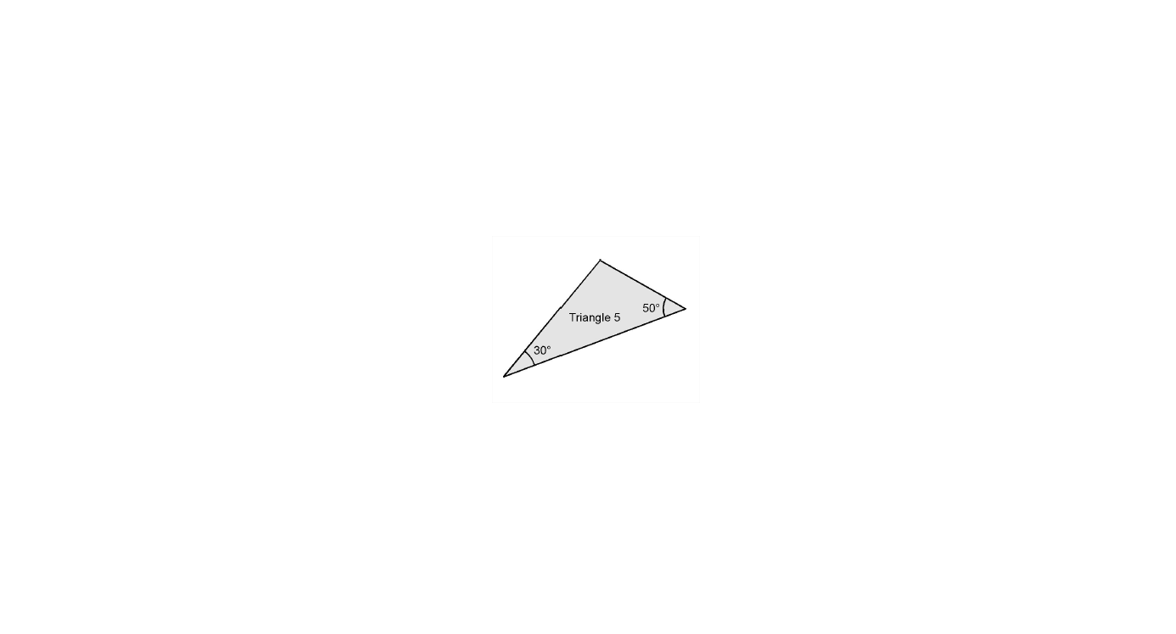
Sans mesurer de longueurs, construire un triangle pouvant s’y associer. Pour cela, on pourra s’inspirer du positionnement des paires de triangles de l’étape 1 qui sont collées. Expliquer comment la construction a été faite.
|
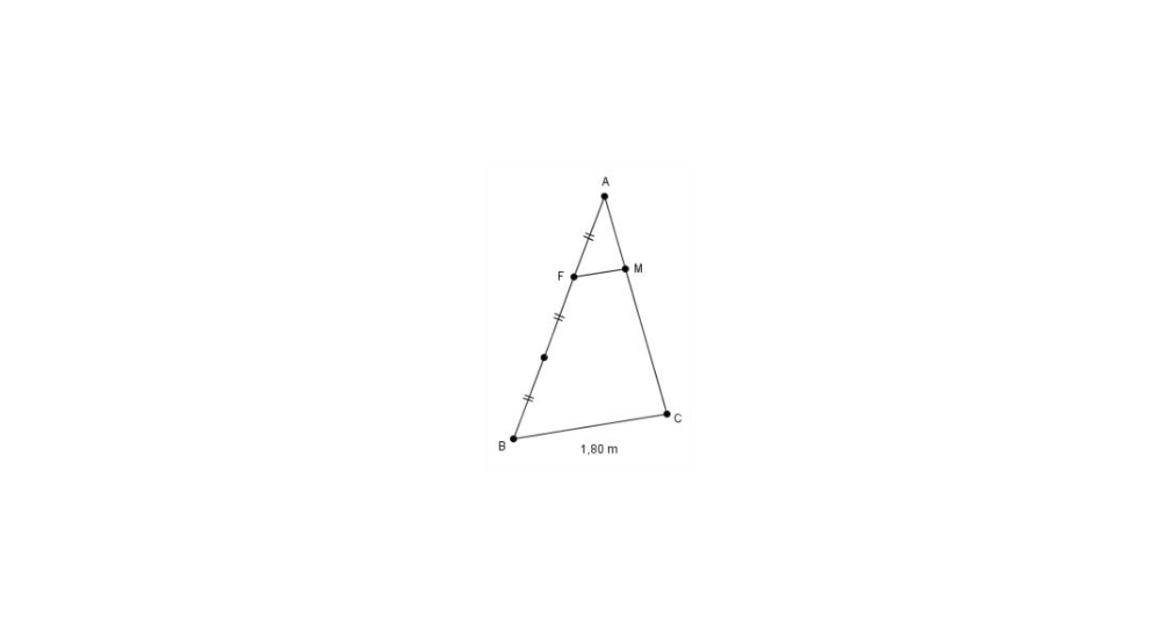
3ème étape : Sur la figure ci-contre :
Calculer la longueur FM si BC = 1,80 m. |
Fichiers joints :
Enoncé de l’activité « des couples de triangles »
1_Activité_des couples de triangles.docx (191.72 Ko)Document de travail de l’activité « des couples de triangles » par l’IREM d’Aquitaine et d’Orléans avec le scénario de la séance, les prérequis, le matériel et la description et l’analyse de la séance en s’appuyant sur des copies d’élèves
Des extraits de copies d’élèves de 3ème ayant traité cette activité cette année.
3_Extraits de copies d'élèves.pdf (882.08 Ko)
Modalités de mise en œuvre :
Tout au long de l’activité, des cahiers d’élèves peuvent être scannés (avec une réglette scanner ou avec ChingView) et projetés en classe.
Cela permet de montrer à la 1ère étape les différentes associations proposées et leurs justifications.
A la 2ème étape on projette ainsi différentes constructions proposées par les élèves, afin d’élargir le théorème de Thalès à toutes les configurations possibles : triangles emboîtés et configuration « papillon ».
Pour aller plus loin :
De nombreuses ressources sur le thème « Proportionnalité et géométrie plane au cycle 4 » sont disponibles sur le site académique en suivant ce lien :
https://pedagogie.ac-toulouse.fr/mathematiques/node/456
Elles s’appuient sur les extraits de programmes relatifs au thème D « Espace et Géométrie » et sur le document d’accompagnement « Espace et Géométrie » au cycle 4 pour fournir :
- Une proposition de progression
1. Les triangles semblables
2. Les agrandissements et réductions de figures planes
3. Les agrandissements et réductions de triangles, et la caractérisation des triangles semblables par la proportionnalité
4. Le cas particulier du théorème de Thalès, en configuration « triangles emboîtés » puis « papillon »
5. Les homothéties
6. La réciproque du théorème de Thalès
7. Les rapports trigonométriques
8. Vers les fonctions linéaires
- Des activités d’introduction, des définitions, propriétés et démonstrations sur chacun de ces thèmes avec des figures évolutives Geogebra associées.
